Python is fast becoming the language of choice for Data Scientists. This is driven by two forces. The first is that Python is free. The second is that its libraries are also free. Whether you're part of a business, a student at school or university, or a lone ranger (sorry), it's all free. The open-source mentality is important, and many people and organisations bundle up and publish their code as libraries. There is now a rich ecosystem of well-documented, well-maintained libraries to do just about everything under the sun. At last count, PyPI currently hosts over 180,000 packages.
Being suspicious of black-boxes
The Python community moves quickly, but Data Science moves faster. Machine Learning (ML) approaches to regression and decision trees have been superseded in many peoples' minds by new and sexy algorithms. There are hundreds of blogs discussing which sort of recurrent neural net to use for your classification problem; all made easy by Python's scikit-learn or Keras integration (or TensorFlow/Theano for the brave). This is pretty incredible: what would have once taken a great deal of specific expertise to build can now be achieved by a hobbyist in about 3 lines of code. There aren't so many written about the old-school approaches.
This "democratisation" of sophisticated ML is mostly a good thing, but it's not entirely a good thing. The conscientious Data Scientist should always exercise due care that, when deploying a heavy-duty model, they have chosen an architecture/algorithm for good reason. This should be in spite of its complexity; and not simply vanity's sake, or because it's the algo du jour. As a rule of thumb, complexity is inversely proportional to (i) transparency and (ii) computational efficiency, which are always more important than being able to say, "I used a convolutional neural net". And because of this, it can be horrible to debug highly complex deployments or to diagnose their unexpected behaviour. Never use a sledge-hammer to crack a walnut, you walnut.
From ML to NumPy
Seemingly simple or older ML algorithms have stood the test of time, and so should not be overlooked. The optimisation calculations behind many ML libraries relies heavily on NumPy. So, as something of an allegory (but one which is intimately related), we should also take the time to celebrate the every day heroes that make programming in Python possible. And in my experience, few owe little to NumPy. Just as the humble (noble) decision-tree is a "golden oldie" in ML, there may be friends you never knew you had in Python. NumPy, SciPy and Matplotlib are three that spring to mind: and if you download Python from Anaconda (or WinPython, Enthought's Canopy, and Python(x,y), to name a few popular distributions), these will come pre-installed: you can ad hoc pip install everything else you may need).
But NumPy is special. It's not particularly flashy, and it's often overlooked when proclaiming the benefits of the language, but it's integral to writing high-performance code in Python. In this blog, we'll discuss this un-sung hero: what it's doing under the hood, what it's good at, and where it's superseded.
NumPy does numerical calculations. As such, it is short for Numerical Python, and it integrates closely with the other two packages mentioned above. The discerning may ask, "Python can do numerical calculations natively, so why bother with NumPy?" The answer is that Python is slow. There are two main reasons which we will discuss in some detail.
Variable definitions in an interpreted language
Python is written in C, and uses a C-based interpreter, most often CPython, to execute lines of code. We don't need to declare (or even know) what variables types are before we initialise (assign) them; a variable type is inferred by the interpreter when the line of code involving this object is executed. A happy side-effect is that we do not need to manage the memory in the same way as we do in C. That means no more unsigned char or long long int, no more malloc or free. This simplicity is very desirable. Life is good.
CPython generally chooses the most appropriate variable type. Executing the line x=1 stores the integer at the "name" x (which defines a unique pointer to the integer in memory). Of course, the most memory-efficient way to store this integer is as a single bit object, and x.bit_length() confirms this: x=2 is initialised as a two bits. Neat.
The problem is there is an overhead to determining how best to store a variable which is parsed and this quickly adds up when you do this many times, for example, doing an operation to each value in a long list of values. NumPy empowers us to manually override the variable types to remove this computational overhead. Moreover, a Python list is nothing more than a list of pointers to objects somewhere else in memory. But NumPy's own list-like object, ndarray, is densely packed in memory and of a uniform variable type. Operations on data stored in this way can be eminently optimised by the CPU, see principle of locality. If it is possible to "vectorise" a problem, encoding data types with NumPy may increase the performance by orders of magnitude.
Parallelising numerical operations in Python
This is a pain in Python, because of the global interpreter lock (GIL). In brief, (a single) CPython (instance) forbids two processors from doing things at the same time to avoid race conditions. Whether or not a GIL is a good idea divides opinion (see StackOverflow for lively and amusing debate on the matter). Wherever possible, NumPy elegantly side-steps the GIL.
For a subset of matrix algebra, computing various operations is so common that there exists a highly performant, highly parallelised, compiled method. Basic Linear Algebra Subprograms (BLAS) is a library of sorts, written in C (or another compiled language), which can be called by NumPy via an API. How BLAS works depends on the distribution (run numpy.__config__.show()), and is not for here anyway. The point is that by outsourcing the heavy-lifting to this compiled code, NumPy can lift the GIL early, CPython can continue to execute threads, and the outsourced numerical calculation is executed (in general in parallel) on the remaining hardware.
This all sounds complicated as hell. But not for us, NumPy makes this easy. It knows what hardware we have available on our machine, and (on the fly) it calculates how best to distribute the computation, if at all. So all we need to do is to call the NumPy method and if a BLAS speed-up is possible, NumPy will take care of the rest. NumPy currently integrates BLAS for various (Level 1; linear time) operations including inner products and norms, and also some higher polynomial time operations via SciPy (scipy.linalg.blas), including matrix multiplication.
Prove it
We can illustrate the point by defining a dot product in four different ways: (i) the Python list dot: the most basic type where zipped lists are multiplied and summed element-wise, (ii) the naive NumPy dot: the same, except first the arrays are encoded explicitly as NumPy arrays, (iii) the manual NumPy dot: matrix multiplication is outsourced to NumPy, but the sum method is called on a temporary data object, and (iv) the (native) NumPy method, employing numpy.dot().
# (i) Python list dot
def python_list_dot(x1,x2):
summ = 0
for xx1,xx2 in zip(x1,x2):
summ += xx1 * xx2
return summ
# (ii) Naive NumPy dot
def np_naive_dot(x1,x2):
x1 = np.array(x1)
x2 = np.array(x2)
summ = 0
for xx1,xx2 in zip(x1,x2):
summ += xx1 * xx2
return summ
# (iii) Manual NumPy dot
def np_manual_dot(x1,x2):
xx1 = np.array(x1)
xx2 = np.array(x2)
return np.multiply(xx1,xx2).sum()
# (iv) (Native) NumPy dot
def np_dot(x1,x2):
return np.dot(x1,x2)By using a function similar to %timeit, it is possible to record how long each function call takes to execute. Below is the mean wall time (of 20 identical calls) plotted against complexity, where complexity is defined as len(x1). x1 and x2 are lists of random integers.
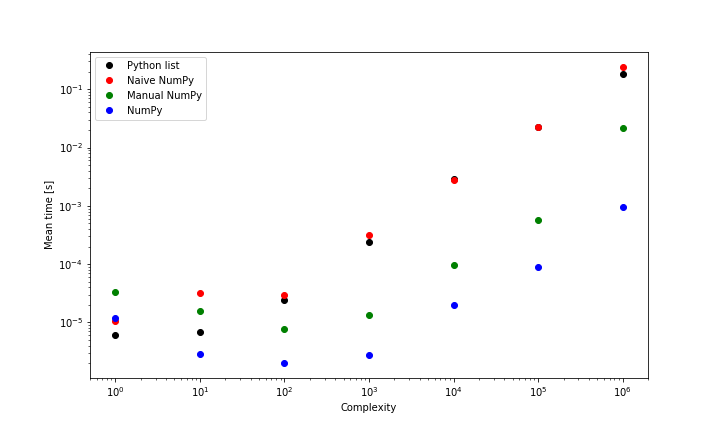
The Python list (i) and naive NumPy (ii) approaches are least performant, since both functions enforce element-wise multiplication which is slow and NumPy is unable to use its BLAS functionality. In fact, (i) will always outperform (ii), since while both of them are element-wise, (ii) has an extra (superfluous) NumPy encoding step; this is clearest for low-complexity calculations. On the other hand, the most performant method; the numpy.dot() (iv) is > 100x faster than these on a list of 1,000,000 elements. Finally, the manual NumPy (iii) calculation lies in the middle, since while it uses the sophisticated functionality discussed above, it requires writing the product to memory before summation. The native NumPy dot product is always faster (for lists of >1 element), particularly for larger calculations.
Summary
At this late stage, the sceptical reader may recall my earlier swipes at colleagues who deliberately opt for complex solutions when a simple one will suffice. And NumPy is, after all, phenomenally complicated. To clarify, understanding what software is doing is the most important thing for Data Scientists. Conceptually, what NumPy does is exceedingly straightforward: NumPy does calculations with numbers in tables. Learning precisely how software is implemented to do that something is more often the remit of a Data Scientist when they care especially about performance, or when they're frustrated by functionality that is not yet implemented, or perhaps when they wish to contribute to the codebase.
So, while it is clear that NumPy is a complex computational tool, this is all under the hood. Its complexity is a managed one; bundled up in a well-maintained, well-documented package. And besides, it is transparent enough for the interested. So don't fight it, NumPy has been designed to make our lives easier.


